It's all regression

Presentation in terms of algebra

	Quantitative	Categorical
Quant.	\(b_1 = \frac{n\sum xy - \sum x \cdot \sum y}{n \sum x^2 - (\sum x)^2}\)	\(t = \frac{\bar{x}_1 - \bar{x}_2 - (\mu_1 - \mu_2)}{\sqrt{\frac{s_p^2}{n_1} + \frac{s_p^2}{n_2}}}\)
………….	……………………………………	……………………………………….
Categ.	??????	\(z = \frac{(\hat{p_1} - \hat{p_2}) - (p_1 - p_2)}{\sqrt{\frac{\bar{p}\bar{q}}{n_1} + \frac{\bar{p}\bar{q}}{n_2}}}\)

… and associated distributions: t and z

Data beats formulas

	Quantitative	Categorical
Quant.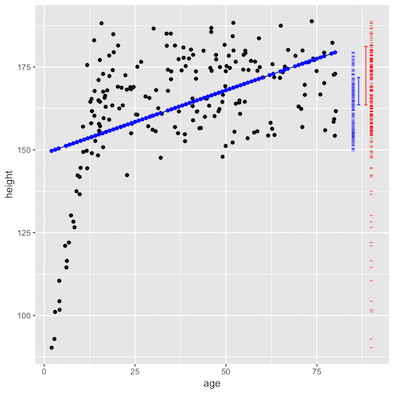
………….	……………………………………	……………………………………….
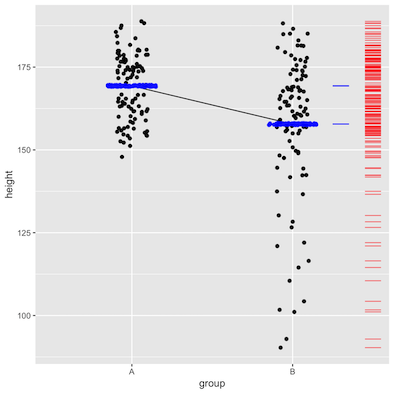
Categ.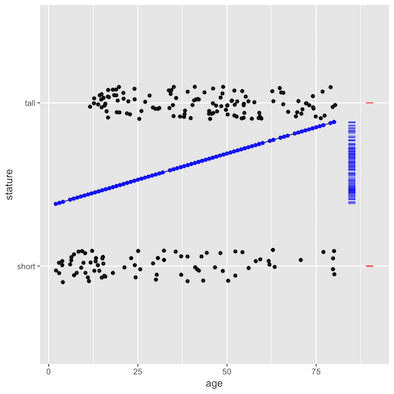

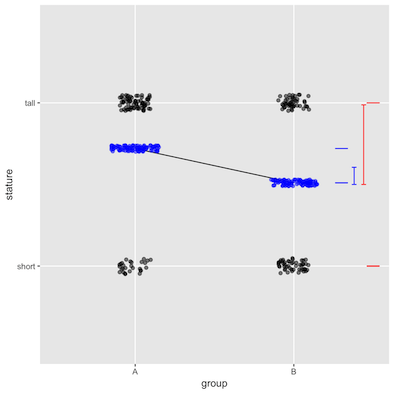Raw and model values

The error bars show the size of the standard deviation.

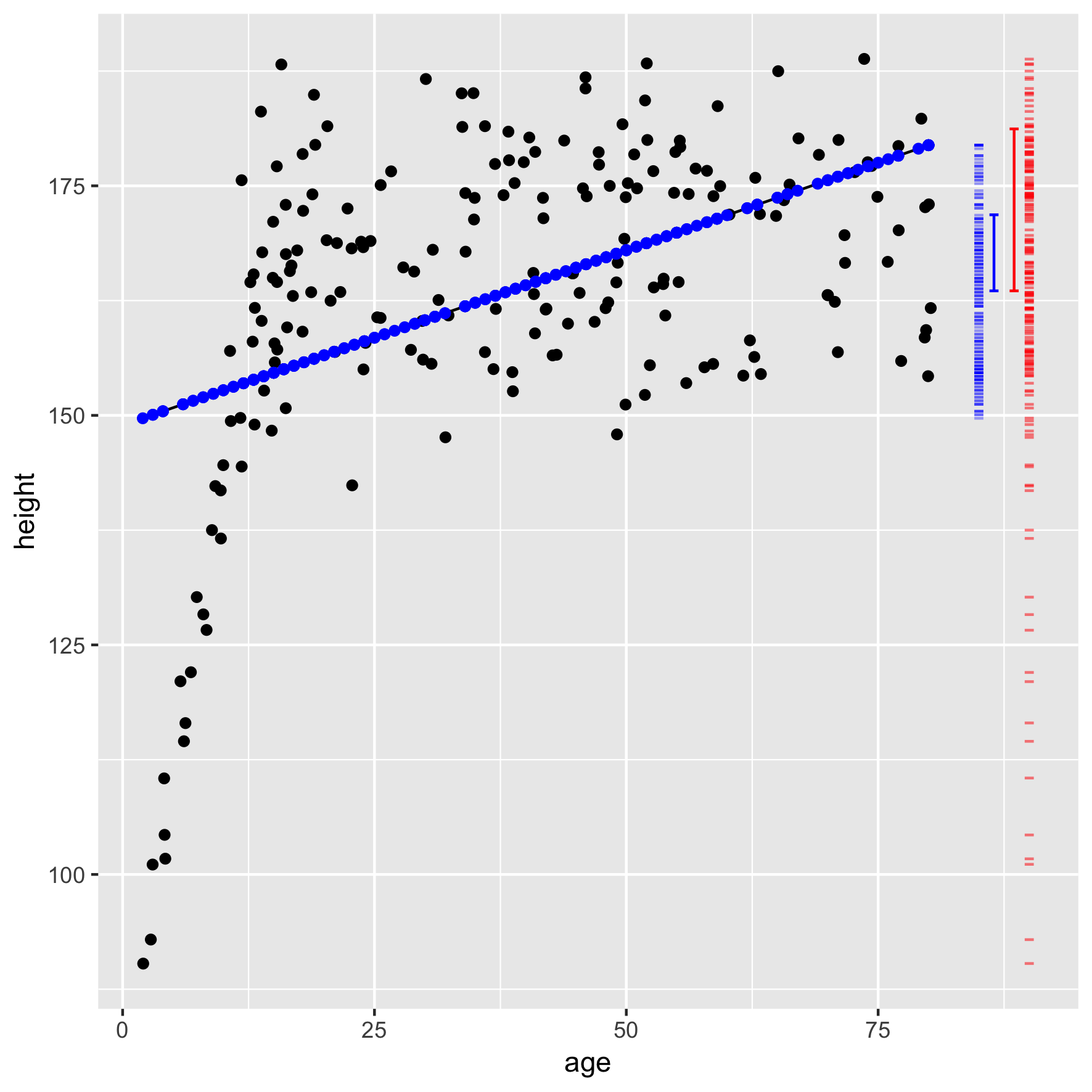
The formal inference procedure

1. Measure the effect size. Call it \(\beta\):
   • slope for Quant vs Quant or Cat vs Quant
   • difference for Quant vs Cat or Cat vs Cat
2. Take the ratio of the model-value standard deviation to the raw-value standard deviation. Call this ratio \(R\).

3. Compute the ratio of “explained” to “unexplained”: \[F = (n-1) \frac{R^2}{1 - R^2}\]

Eyeballing from the four models (which had n = 200)…

4. Confidence interval on \(\beta\) is always \[CI_\beta = \beta (1 \pm 2 / \sqrt{F})\]

5. p-value … Look up in this graph.

Freebies:

• correlation coefficient \(r = \sqrt{R^2}\), where the \(\pm\) branch is based on the slope.
• Prefer t? It’s \(t = \sqrt{F}\). But F is more general than t.